LA REGRESSION LINEAIRE

Vous rêvez de développer un programme de Machine Learning pouvant prédire le cours de la bourse, le prix d’un appartement, ou bien pour étudier le réchauffement climatique ? Alors la régression linéaire est le choix parfait pour vous lancer

Rappel des 4 étapes indispensables en Supervised Learning

Rappelez-vous, pour résoudre un problème d’apprentissage supervisé, nous avons vu qu’il faut procéder en 4 étapes :

Disposer d’un Dataset $(x, y)$ où $x$ sont les features et $y$ est la target
Développer un Modèle dont les paramètres sont à trouver
Définir une Fonction Coût qui mesure l’erreur entre le modèle et les valeurs de $y$ du Dataset
Utiliser un Algorithme d’Apprentissage qui cherche le modèle (en réalité les paramètres) qui minimisent la Fonction Coût, c’est-à-dire qui nous donne le modèle aux plus petites erreurs.

Mon petit conseil

Lorsque vous développez un programme de Machine Learning, prenez toujours une feuille et un stylo et écrivez ces 4 étapes :

Combien y a-t-il d’exemples et de variables dans votre Dataset ?
Quelle est la fonction que vous avez choisie pour votre modèle ?
Quelle Fonction Coût avez-vous sélectionnez ?
Et quel est l’algorithme d’apprentissage que vous utilisez ?

Et dans cet article, nous allons justement suivre cette démarche en procédant étape par étape.

Let’s go !

1. Le Dataset d’une Régression Linéaire simple

Dans cet article, nous allons faire simple, dans le sens où nous allons voir comment développer un modèle de Machine Learning à partir d’un Dataset à une seule variable $x_1$ (que l’on notera simplement $x$ ). On aura donc un Dataset avec $m$ exemples et $n=1$ « feature » variable.

$y$	$x$
$y^{(1)}$	$x^{(1)}$
$y^{(2)}$	$x^{(2)}$
$y^{(3)}$	$x^{(3)}$
…	…
$y^{(m)}$	$x^{(m)}$

Pour éviter de rester trop abstrait, on peut très bien imaginer que ce Dataset représente le prix d’un appartement $y$ en fonction de sa surface habitable $x$ dans une ville donnée. Ce Dataset nous pourrait nous donner le nuage de point suivant :

Prix y en €	Surface x $m^2$
350,000	100
160,000	50
280,000	80
…	…
235,000	75

2. Le Modèle de Régression Linéaire Simple

En voyant notre nuage de point, on dirait clairement qu’il suit une tendance linéaire, voilà pourquoi nous allons développer un modèle… linéaire ! Notre modèle : $f(x) = ax + b$ .

Oui oui ! C’est une fonction affine ! Qui aurait cru que l’on pourrait faire du Machine Learning avec des maths aussi simples ?!

Pour le moment, nous ne connaissons pas la valeur des paramètres $a$ et $b$ , il est donc impossible de tracer une bonne droite sur le nuage de point, à moins de choisir des paramètres au hasard. Ce sera le rôle de la machine d’apprendre ces valeurs en minimisant la fonction coût. En parlant de fonction coût, il est temps de passer à l’étape 3 !

3. La Fonction Coût : L’Erreur Quadratique Moyenne

Pour rappel, la fonction coût nous permet d’évaluer la performance de notre modèle en mesurant les erreurs entre $f(x^{(i)})$ et $y^{(i)}$ . La question que l’on se pose est: Comment mesurer ces erreurs ? Je vous le dévoile avec l’analogie qui suit.

Imaginez visiter un appartement à 200000 €. Votre modèle de Machine Learning prédit que cet appartement vaut 300000 €. Vous pourrez conclure que votre modèle fait donc une erreur de 300000 – 200000 = 100000 €.

Ainsi, on pourrait se dire que pour mesurer nos erreurs, il faut faire calculer la différence $f(x) - y$ . Cependant, si votre prédiction $f(x)$ est inférieure à $y$ , alors cette erreur est négative, ce qui n’est pas pratique (personne ne dit : ” J’ai fait une erreur de négatif 100000 € “)

Alors, pour mesurer les erreurs entre les prédictions $f(x)$ et les valeurs $y$ du Dataset, on calcule le carré de la différence : $(f(x) - y)^2$ . C’est au passage ce qu’on appelle la norme euclidienne, qui représente la distance directe entre $f(x)$ et $y$ dans la géométrie euclidienne (la géométrie qu’on utilise au quotidien)

Pour la régression linéaire, la fonction Coût $J$ va être la moyenne de toutes nos erreurs, c’est-à-dire :

$J = \frac{[f(x^{(1)}) - y^{(1)}]^2 + ... + [f(x^{(m)}) - y^{(m)}]^2}{m}$

Par convention on écrit cette fonction de la manière suivante, en rajoutant un coefficient $\frac{1}{2}$ pour simplifier un calcul de dérivée qui viendra par la suite.

$J(a, b) = \frac{1}{2m} \sum_{i = 1}^{m}(f(x^{(i)}) - y^{(i)})^2$

$J(a, b) = \frac{1}{2m} \sum_{i = 1}^{m}(ax^{(i)} + b - y^{(i)})^2$

Cette fonction porte un nom : en français on l’appelle l’Erreur Quadratique Moyenne, et en anglais elle s’appelle Mean Squared Error.

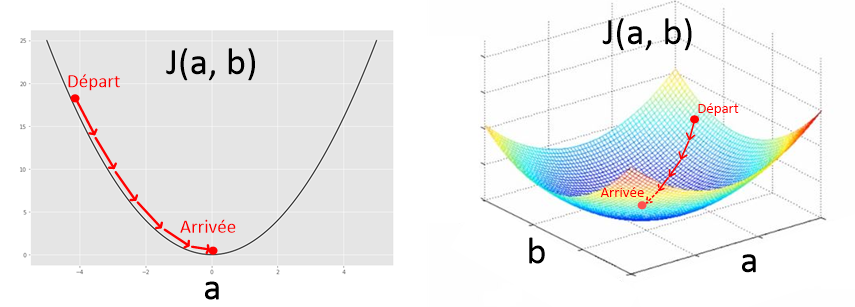
Dans le cas d’une régression linéaire, cette fonction ne dépend que de deux paramètres : $a$ et $b$ . Quand on l’observe, elle a l’apparence d’une belle vallée bien lisse. On dit que c’est une fonction convexe. Cette propriété est très importante pour s’assurer de converger vers le minimum avec l’algorithme de la descente de gradient que nous verrons dans le prochain article.

4. L’algorithme d’apprentissage

Pour rappel, on dit que la machine apprend quand elle trouve quels sont les paramètres du modèle qui minimisent la fonction Coût. On cherche donc à développer un algorithme de minimisation. La bonne nouvelle, c’est qu’il existe un paquet de méthodes de minimisation (méthode des moindres carrés, méthode de Newton, Gradient Descent, Simplex, etc.)

Pour un modèle de régression linéaire, on utilise le plus souvent la méthode des moindres carrés (quand le problème est simple) et l’algorithme de Gradient Descent (pour les régressions plus compliquée). Le Gradient Descent, que nous allons décortiquer en détail dans le prochain article, permet de converger progressivement vers le minimum de n’importe quelle fonction convexe (comme la Fonction Coût) en suivant la direction de la pente (le gradient) qui descend, d’où son nom de Gradient Descent.

Régression linéaire simple : En Conclusion

Avec la régression linéaire, nous avons vu comment mettre en pratique les 4 étapes pour résoudre un problème d’apprentissage supervisé. Ce même mécanisme sera utilisé pour élaborer un système de reconnaissance vocale, de vision par ordinateur ou des chatbots. Il sera juste question d’utiliser un autre modèle avec une autre fonction Coût. Dans le prochain article je vous expliquerai dans les détails comment fonctionne l’algorithme de Gradient Descent, ce qui nous permettra de compléter notre algorithme de Machine Learning pour la régression linéaire, et de pouvoir enfin écrire notre premier programme de Machine Learning !

Mon conseil : Notez toujours sur une feuille vos différentes équations ainsi que les dimensions de votre Dataset avant de passer à la programmation. Ce geste simple peut vous faire gagner un temps considérable en évitant les bugs liés aux erreurs de maths.

Si cet article vous a plu, merci de le partager et merci de me laisser un commentaire !

A bientôt les Data Scientists !

Dans les derniers articles de cette formation, vous avez vu les équations pour écrire un programme de Régression Linéaire complet, puis vous avez appris à vous servir des matrices. Il est grand temps de combiner les deux pour aboutir à la vraie régression linéaire, celle qui est réellement implémentée dans un programme de Machine Learning !

Pourquoi écrire les équations sous forme matricielle ?

À l’heure actuelle, voici votre programme de régression linéaire écrit sur papier. Ce programme apprend, grâce à la Descente de Gradient, quels sont les paramètres $a$ et $b$ qui donnent le meilleur modèle $f(x) = ax + b$ .

[image bientôt disponible]

En revanche, ce programme n’est pas du tout pratique à implémenter sous cette forme.

Pour commencer, le calcul des Gradients $\frac{\partial J(a, b)}{\partial a,b}$ implique de faire la somme des $x^{(i)} \times (ax^{(i)} + b - y^{(i)})$ pour toutes les valeurs de notre Dataset, valeur après valeur… Bonjour la galère !

Dans la même lancée, on ne peut utiliser notre modèle $f(x) = ax+b$ que sur une valeur $x^{(i)}$ à la fois. Donc si vous voulez calculer des millions de prédictions $f(x)$ , vous devez effectuer des millions de fois ce calcul, pour chaque valeur $x^{(i)}$ désirée…

Vous voulez une aspirine ? N’en prenez surtout pas, ça n’est pas la peine ! Car il suffit de reformuler nos équations sous forme matricielle pour calculer d’une seule traite le Gradient, la Fonction Coût, et le modèle sur toutes les données de notre Dataset. Voici comment procéder.

1. Transférer le Dataset dans des matrices X, y

En présence d’un Dataset $(x, y)$ qui contient $m$ exemples et $n$ features, on transfert toutes les données $y^{(i)}$ dans un vecteur $Y$ de dimension $(m \times 1)$ et toutes les données $x^{(i)}$ dans une matrice $X$ à laquelle on ajoute une colonne biais (c’est une colonne remplie de « 1 »). La matrice $X$ est donc de dimension $(m \times n+1)$ et. Dans le cas de la régression linéaire à une seule variable, on a $n=1$ et donc la matrice $X$ est de dimension $(m \times 2)$ . Vous allez comprendre l’utilité de la colonne biais dans un instant.

$X = \begin{bmatrix} x^{(1)} & 1\\ x^{(2)} & 1\\x^{(3)} & 1\\ ... & ...\\ x^{(m)} &1 \end{bmatrix}$

$Y = \begin{bmatrix}y^{(1)} \\y^{(2)} \\y^{(3)} \\ ... \\ y^{(m)} \end{bmatrix}$

[image bientôt disponible]

2. Le modèle $F = X.\theta$

À l’heure actuelle, le modèle linéaire $f(x^{(i)}) = ax^{(i)} + b$ ne permet que d’effectuer le calcul d’une prédiction à la fois, selon une valeur $x^{(i)}$ unique. Pour remédier à ce problème, il suffit de créer un vecteur $F$ de dimension $(m \times 1)$ qui contient toutes les prédictions :

$F = \begin{bmatrix} f(x^{(1)}) \\ f(x^{(2)}) \\ f(x^{(3)})\\ ... \\ f(x^{(m)}) \end{bmatrix}$

Pour calculer ce vecteur, on utilise la formule suivante : $F = X.\theta$ où $\theta = \begin{bmatrix} a \\ b \end{bmatrix}$ est le vecteur paramètre qui contient tous les paramètres de notre modèle.

On a donc le produit matriciel :

$F = X.\theta = \begin{bmatrix} x^{(1)} & 1\\ ... & ...\\ x^{(m)} &1 \end{bmatrix} . \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} ax^{(1)} + 1\times b\\ ... \\ ax^{(m)} +1\times b \end{bmatrix} = \begin{bmatrix} f(x^{(1)}) \\ ... \\ f(x^{(m)}) \end{bmatrix}$

Note : la colonne biais de la matrice $X$ permet donc d’effectuer le produit matriciel $X.\theta$ . On dit également que le paramètre b est un paramètre biais.

3. La Fonction Coût $J(\theta)$

A l’heure actuelle, la fonction coût que nous avons pour la régression linéaire est l’erreur quadratique moyenne :

$J(a, b) = \frac{1}{2m} \sum_{i = 1}^{m}(ax^{(i)} + b - y^{(i)})^2$

On sait désormais que $ax^{(i)} + b$ peut s’écrire sous la forme $X.\theta$ . Concernant $y^{(i)}$ , nous allons créer un vecteur $Y$ qui contient tous les $y^{(i)}$ du Dataset :

$Y = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\...\\y^{(m)} \end{bmatrix}$

Les vecteurs $Y$ et $X.\theta$ sont tous 2 de dimensions $(m \times 1)$ , on peut donc effectuer le calcul $X.\theta - Y$ .

La suite est simple : on prend le carré de chaque élément du vecteur $X.\theta - Y$ , puis on fait la somme de chacun de ces éléments, avant de diviser le tout par $\frac{1}{2m}$ .

La forme matricielle de la fonction coût est alors :

$J(\theta) = \frac{1}{2m} \sum (X.\theta - Y)^2$

Note : $J$ n’est ni une matrice, ni un vecteur. C’est un scalaire (un nombre). En effet, cela n’aurait pas de sens de mettre $J(a, b)$ sous forme de matrice, car la fonction coût permet d’exprimer avec une valeur unique la performance de notre modèle. A la limite, on pourrait dire que l’on cherche à écrire $J(a, b)$ comme une matrice de dimension $(1 \times 1)$ , c’est-à-dire une matrice ne contenant qu’un nombre.

4. Les Gradients

Pour calculer les gradients, nous devions auparavant définir une formule spécifique pour chaque paramètre.

$\frac{\partial J(a, b)}{\partial a} = \frac{1}{m} \sum_{i = 1}^{m} x^{(i)} \times (ax^{(i)} + b - y^{(i)})$

$\frac{\partial J(a, b)}{\partial b} = \frac{1}{m} \sum_{i = 1}^{m} (ax^{(i)} + b - y^{(i)})$

Il est possible de rassembler le calcul de ces 2 gradient en un vecteur gradient $\frac{\partial J(\theta)}{\partial \theta}$ :

$\frac{\partial J(\theta)}{\partial \theta}= \begin{bmatrix} \frac{\partial J(a, b)}{\partial a} \\ \frac{\partial J(a, b)}{\partial b} \end{bmatrix}$ .

Note : ce vecteur est donc de dimension $(2 \times 1)$ ou bien $(n+1 \times 1)$

Pour obtenir ce vecteur on écrit la formule suivante :

$\frac{\partial J(\theta)}{\partial \theta} = \frac{1}{m} X^T.(X.\theta - Y)$

Je me doute que vous vous posez 2 questions en particulier :

Que fait $X^T$ au milieu de cette expression ?
Où est passée la somme $\sum_{i = 1}^{m}$ ?

Pour répondre à ces deux questions, commençons par examiner ce que nous connaissons déjà. Notre expression commence par $\frac{1}{m}$ , qui est commun à nos deux gradients. C’est donc logique de le retrouver dans l’expression $\frac{\partial J(\theta)}{\partial \theta}$ .

Ensuite, le terme $(ax^{(i)} + b - y^{(i)})$ est lui aussi commun aux deux gradients, et on sait qu’on peut l’écrire sous forme matricielle : $X.\theta - Y$ . Le résultat est de dimension $(m \times 1)$

1. Pourquoi $X^T$ ?

Essayez de remarquer le lien entre les lignes de la transposée de $X$ …

$X^T = \begin{bmatrix} x^{(1)} & x^{(2)} & … & x^{(m)} \\ 1&1&…&1 \end{bmatrix}$

Et les lignes du vecteur $\frac{\partial J(\theta)}{\partial \theta}$ …

$\frac{\partial J(\theta)}{\partial \theta} = \begin{bmatrix} \frac{1}{m} \sum_{i = 1}^{m} x^{(i)} \times (ax^{(i)} + b - y^{(i)}) \\ \frac{1}{m} \sum_{i = 1}^{m} 1 \times (ax^{(i)} + b - y^{(i)} \end{bmatrix}$

Vous l’avez ? C’est dans la première ligne de $\frac{\partial J(\theta)}{\partial \theta}$ que l’on trouve le facteur $x^{(i)}$ , et c’est aussi dans la première ligne de $X^T$ que ce situent tous les $x^{(i)}$ !

De la même manière, dans la deuxième ligne de $\frac{\partial J(\theta)}{\partial \theta}$ on trouve un facteur 1, comme dans $X^T$ .

Ainsi, en effectuant le produit matriciel $X^T.(X.\theta - Y)$ on obtient le vecteur :

$X^T.(X.\theta - Y) = \begin{bmatrix} \sum_{i = 1}^{m} x^{(i)} \times (ax^{(i)} + b - y^{(i)})\\ \sum_{i = 1}^{m} 1 \times (ax^{(i)} + b - y^{(i)})\end{bmatrix}$

2. C’est dans ce vecteur que la somme $\sum_{i = 1}^{m}$ apparaît !

Eh Oui ! C’est juste les lois du calcul matriciel ! C’est pour ça que lire l’article précédent, dédié au calcul matriciel, est vraiment important ! Pour rappel voici en dessin ce qui se passe lors du produit matriciel:

[ [image bientôt disponible] X.T (XO – Y)]

Note : La matrice $X^T$ est de dimension $(n+1 \times m)$ . Le résultat du produit matriciel est donc de dimension $(n+1 \times 1)$ , ce qui concorde avec la dimension finale du vecteur gradient $\frac{\partial J(\theta)}{\partial \theta}$ .

Oui ça fait beaucoup de maths ! Pfiou…

J’espère que vous êtes toujours avec moi, parce que nous touchons notre objectif du bout des doigts. Il ne reste plus qu’à formuler l’algorithme de la descente de gradient sous forme matricielle et le tour est joué !

5. La Descente de Gradient

Pour rappel, l’algorithme de la Descente de Gradient met à jour les paramètres $a$ et $b$ de notre modèle de façon itérative avec 2 lignes de calculs :

[image bientôt disponible]

Mais à présent que nous avons créé un vecteur paramètre $\theta = \begin{bmatrix} a \\ b \end{bmatrix}$ et un vecteur gradient $\frac{\partial J(\theta)}{\partial \theta}$ il est possible de résumer l’algorithme de Descente de Gradient sur une seule ligne !

On a :

$\theta = \theta - \alpha \times \frac{\partial J(\theta)}{\partial \theta}$

Note: les dimensions de $\theta$ sont évidemment préservées : $(n+1) \times 1$

La Vraie Régression Linéaire

Croyez-moi, vous venez de passer un cap… En exprimant la Régression Linéaire sous forme matricielle, vous connaissez désormais les équations telles qu’elles sont réellement implémentées dans un programme de Machine Learning :

[image bientôt disponible]

Développer un Modèle polynômial… A suivre !

Ce qui est absolument génial avec ces équations, c’est qu’on peut les utiliser en tant que telles pour développer des modèles polynômiaux plus complexes que le modèle linéaire que vous connaissez aujourd’hui.

Par exemple voici à quoi ressemble un programme de Régression polynômiale de degré 3 avec les anciennes équations… Bon Courage…

[image bientôt disponible]

Et maintenant voici à quoi ressemble ce programme sous forme matricielle.

[image bientôt disponible]

OUI ! Ce sont les mêmes équations qu’avant ! Quand je vous disais que les matrices nous simplifient la vie !

Dites-moi dans les commentaires quelles applications vous rêvez de développer avec cette technique ! Nous verrons plus en détail comment développer de tels programmes dans un article futur, mais pour l’heure, vous méritez de faire une pause !

Le prochain article de cette formation est une introduction à la programmation en Python, vous êtes libre de l’ignorez si vous maitriser déjà les bases de la programmation !

Si cet article vous a plu, merci de le partager avec vos amis et collègues.

Rechercher dans ce blog

GENIE LOGICIEL ET SYSTEMES EMBARQUES