Comment fonctionne l'optimise d'Adam

Introduction en douceur à l'algorithme d'optimisation Adam pour le Deep Learning

Le choix de l'algorithme d'optimisation pour votre modèle d'apprentissage en profondeur peut faire la différence entre de bons résultats en minutes, heures et jours.

L' algorithme d'optimisation Adam est une extension de la descente de gradient stochastique qui a récemment été plus largement adoptée pour les applications d'apprentissage en profondeur dans la vision par ordinateur et le traitement du langage naturel.

Dans cet article, vous obtiendrez une introduction en douceur à l'algorithme d'optimisation Adam à utiliser dans l'apprentissage en profondeur.

Après avoir lu cet article, vous saurez:

• Qu'est-ce que l'algorithme Adam et certains avantages de l'utilisation de la méthode pour optimiser vos modèles.
• Comment fonctionne l'algorithme d'Adam et en quoi il est différent des méthodes associées d'AdaGrad et de RMSProp.
• Comment l'algorithme Adam peut être configuré et les paramètres de configuration couramment utilisés.

Lancez votre projet avec mon nouveau livre Better Deep Learning , comprenant des didacticiels étape par étape et les fichiers de code source Python pour tous les exemples.

Commençons.

Qu'est-ce que l'algorithme d'optimisation Adam?

Adam est un algorithme d'optimisation qui peut être utilisé à la place de la procédure classique de descente de gradient stochastique pour mettre à jour les poids de réseau itératifs en fonction des données d'apprentissage.

Adam a été présenté par Diederik Kingma d'OpenAI et Jimmy Ba de l'Université de Toronto dans leur article (affiche) ICLR 2015 intitulé « Adam: une méthode pour l'optimisation stochastique ». Je citerai libéralement leur article dans cet article, sauf indication contraire.

L'algorithme s'appelle Adam. Ce n'est pas un acronyme et ne s'écrit pas «ADAM».

… Le nom Adam est dérivé de l'estimation du moment adaptatif.

Lors de l'introduction de l'algorithme, les auteurs énumèrent les avantages intéressants de l'utilisation d'Adam sur des problèmes d'optimisation non convexes, comme suit:

• Simple à mettre en œuvre.
• Efficace en termes de calcul.
• Peu de besoins en mémoire.
• Invariant à la remise à l'échelle diagonale des dégradés.
• Bien adapté aux problèmes importants en termes de données et / ou de paramètres.
• Convient aux objectifs non stationnaires.
• Convient aux problèmes avec des gradients très bruyants / ou clairsemés.
• Les hyper-paramètres ont une interprétation intuitive et nécessitent généralement peu de réglages.

Comment fonctionne Adam?

Adam est différent de la descente de gradient stochastique classique.

La descente de gradient stochastique maintient un taux d'apprentissage unique (appelé alpha) pour toutes les mises à jour de poids et le taux d'apprentissage ne change pas pendant l'entraînement.

Un taux d'apprentissage est maintenu pour chaque poids de réseau (paramètre) et adapté séparément à mesure que l'apprentissage se déroule.

La méthode calcule des taux d'apprentissage adaptatifs individuels pour différents paramètres à partir d'estimations des premier et second moments des gradients.

Les auteurs décrivent Adam comme combinant les avantages de deux autres extensions de la descente de gradient stochastique. Spécifiquement:

• Algorithme de gradient adaptatif (AdaGrad) qui maintient un taux d'apprentissage par paramètre qui améliore les performances sur des problèmes avec des gradients clairsemés (par exemple, des problèmes de langage naturel et de vision par ordinateur).
• Propagation de la moyenne quadratique (RMSProp) qui maintient également des taux d'apprentissage par paramètre qui sont adaptés en fonction de la moyenne des amplitudes récentes des gradients pour le poids (par exemple, à quelle vitesse il change). Cela signifie que l'algorithme fonctionne bien sur les problèmes en ligne et non stationnaires (par exemple, bruyant).

Adam se rend compte des avantages d'AdaGrad et de RMSProp.

Au lieu d'adapter les taux d'apprentissage des paramètres en fonction du premier moment moyen (la moyenne) comme dans RMSProp, Adam utilise également la moyenne des seconds moments des gradients (la variance non centrée).

Plus précisément, l'algorithme calcule une moyenne mobile exponentielle du gradient et du gradient carré, et les paramètres beta1 et beta2 contrôlent les taux de décroissance de ces moyennes mobiles.

La valeur initiale des moyennes mobiles et les valeurs bêta1 et bêta2 proches de 1,0 (recommandé) entraînent un biais des estimations de moment vers zéro. Ce biais est surmonté en calculant d'abord les estimations biaisées avant de calculer ensuite les estimations corrigées du biais.

Le document est assez lisible et je vous encourage à le lire si vous êtes intéressé par les détails spécifiques de la mise en œuvre.

Si vous souhaitez apprendre à coder Adam à partir de zéro en Python, consultez le didacticiel:

• Optimisation de la descente de gradient Code Adam à partir de zéro

Adam est efficace

Adam est un algorithme populaire dans le domaine de l'apprentissage profond car il obtient rapidement de bons résultats.

Les résultats empiriques démontrent qu'Adam fonctionne bien en pratique et se compare favorablement aux autres méthodes d'optimisation stochastique.

Dans l'article original, il a été démontré empiriquement qu'Adam montre que la convergence répond aux attentes de l'analyse théorique. Adam a été appliqué à l'algorithme de régression logistique sur les ensembles de données de reconnaissance de chiffres MNIST et d'analyse des sentiments IMDB, un algorithme Perceptron multicouche sur l'ensemble de données MNIST et des réseaux de neurones convolutionnels sur l' ensemble de données de reconnaissance d'image CIFAR-10 . Ils concluent:

En utilisant de grands modèles et ensembles de données, nous démontrons qu'Adam peut résoudre efficacement des problèmes pratiques d'apprentissage profond.

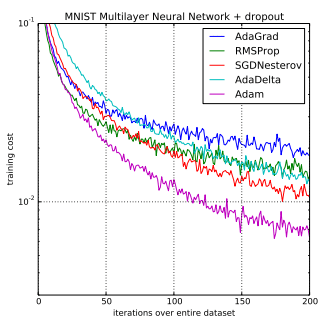
Comparaison d'Adam à d'autres algorithmes d'optimisation entraînant un perceptron multicouche
tiré d'Adam: une méthode pour l'optimisation stochastique, 2015.

Sebastian Ruder a développé une revue complète des algorithmes d'optimisation de descente de gradient modernes intitulée « Un aperçu des algorithmes d'optimisation de descente de gradient », publiée d'abord sous forme d'un article de blog , puis d'un rapport technique en 2016.

Le document est essentiellement une visite des méthodes modernes. Dans sa section intitulée « Quel optimiseur utiliser? «, Il recommande d'utiliser Adam.

Dans la mesure où RMSprop, Adadelta et Adam sont des algorithmes très similaires qui fonctionnent bien dans des circonstances similaires. […] Sa correction de biais aide Adam à surpasser légèrement RMSprop vers la fin de l'optimisation à mesure que les gradients deviennent plus clairsemés. Dans la mesure où, Adam pourrait être le meilleur choix global.

Dans le cours de Stanford sur l'apprentissage en profondeur pour la vision par ordinateur intitulé « CS231n: Réseaux de neurones convolutionnels pour la reconnaissance visuelle » développé par Andrej Karpathy, et al., L'algorithme d'Adam est à nouveau suggéré comme méthode d'optimisation par défaut pour les applications d'apprentissage en profondeur .

Dans la pratique, Adam est actuellement recommandé comme algorithme par défaut à utiliser, et fonctionne souvent légèrement mieux que RMSProp. Cependant, il vaut souvent la peine d'essayer SGD + Nesterov Momentum comme alternative.

Et plus tard déclaré plus clairement:

Les deux mises à jour recommandées à utiliser sont SGD + Nesterov Momentum ou Adam.

Adam est en cours d'adaptation pour des repères dans les articles d'apprentissage en profondeur.

Par exemple, il a été utilisé dans le document « Show, Attend and Tell: Neural Image Caption Generation with Visual Attention » sur l'attention dans le sous-titrage d'images et « DRAW: A Recurrent Neural Network For Image Generation » sur la génération d'images.

Connaissez-vous d'autres exemples d'Adam? Faites-moi savoir dans les commentaires.

Paramètres de configuration Adam

• alpha . Également appelé taux d'apprentissage ou taille de pas. Proportion de mise à jour des poids (par exemple 0,001). Des valeurs plus élevées (par exemple 0,3) se traduisent par un apprentissage initial plus rapide avant la mise à jour du taux. Des valeurs plus petites (par exemple 1.0E-5) ralentissent l'apprentissage tout au long de la formation
• beta1 . Le taux de décroissance exponentielle pour les estimations du premier moment (par exemple 0,9).
• beta2 . Le taux de décroissance exponentielle pour les estimations au second moment (par exemple 0,999). Cette valeur doit être proche de 1,0 sur des problèmes avec un gradient clairsemé (par exemple, des problèmes de PNL et de vision par ordinateur).
• epsilon . Est un très petit nombre pour éviter toute division par zéro dans l'implémentation (par exemple 10E-8).

En outre, la décroissance du taux d'apprentissage peut également être utilisée avec Adam. L'article utilise un taux de désintégration alpha = alpha / sqrt (t) mis à jour à chaque époque (t) pour la démonstration de régression logistique.

L'article d'Adam suggère:

Les bons paramètres par défaut pour les problèmes d'apprentissage automatique testés sont alpha = 0,001, bêta1 = 0,9, bêta2 = 0,999 et epsilon = 10−8

La documentation TensorFlow suggère quelques réglages d'Epsilon:

La valeur par défaut de 1e-8 pour epsilon peut ne pas être une bonne valeur par défaut en général. Par exemple, lors de la formation d'un réseau Inception sur ImageNet, le bon choix actuel est 1.0 ou 0.1.

Nous pouvons voir que les bibliothèques populaires d'apprentissage en profondeur utilisent généralement les paramètres par défaut recommandés par l'article.

• TensorFlow : taux_apprentissage = 0,001, bêta1 = 0,9, bêta2 = 0,999, epsilon = 1e-08.
  Keras : lr = 0,001, bêta_1 = 0,9, bêta_2 = 0,999, epsilon = 1e-08, désintégration = 0,0.
• Blocs : learning_rate = 0,002, beta1 = 0.9, beta2 = 0.999, epsilon = 1e-08, decay_factor = 1.
• Lasagne : taux_apprentissage = 0,001, bêta1 = 0,9, bêta2 = 0,999, epsilon = 1e-08
• Caffe : taux_apprentissage = 0,001, bêta1 = 0,9, bêta2 = 0,999, epsilon = 1e-08
• MxNet : taux_apprentissage = 0,001, bêta1 = 0,9, bêta2 = 0,999, epsilon = 1e-8
• Torche : taux_apprentissage = 0,001, bêta1 = 0,9, bêta2 = 0,999, epsilon = 1e-8

Connaissez-vous d'autres configurations standard pour Adam? Faites-moi savoir dans les commentaires.

Lectures complémentaires

Cette section répertorie les ressources pour en savoir plus sur l'algorithme d'optimisation Adam.

• Adam: une méthode d'optimisation stochastique , 2015.
• Descente de gradient stochastique sur Wikipedia
• Un aperçu des algorithmes d'optimisation de la descente de gradient , 2016.
• ADAM: Une méthode pour l'optimisation stochastique (un examen)
• Optimisation pour les réseaux profonds (diapositives)
• Adam: une méthode d'optimisation stochastique (diapositives).
• Optimisation de la descente de gradient Code Adam à partir de zéro

Connaissez-vous d'autres bonnes ressources sur Adam? Faites-moi savoir dans les commentaires.

Résumé

Dans cet article, vous avez découvert l'algorithme d'optimisation Adam pour l'apprentissage en profondeur.

Plus précisément, vous avez appris:

• Adam est un algorithme d'optimisation de remplacement pour la descente de gradient stochastique pour la formation de modèles d'apprentissage profond.
• Adam combine les meilleures propriétés des algorithmes AdaGrad et RMSProp pour fournir un algorithme d'optimisation capable de gérer des gradients clairsemés sur des problèmes bruyants.
• Adam est relativement facile à configurer là où les paramètres de configuration par défaut fonctionnent bien sur la plupart des problèmes.

Avez-vous des questions?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.